Quantum Key Distribution

The goal of Quantum Key Distribution (QKD) is to generate a secret key (a string of classical bits) that is known by two parties, say Alice and Bob and is unknown to any third party. Alice and Bob do this by first establishing a raw key between them, using the quantum internet. Then, they do classical operations and communication to transform this raw key into a secret, shared key.

There are various ways to establish a raw key. One way is for Alice to send qubits to Bob, where each qubit encodes a classical bit of the raw key. This is done in for example BB84. Another approach is by using entanglement. Alice and Bob create so-called EPR pairs with each other, which they measure on a certain random basis.

In the QKD application that can be run in the Editor, the entanglement-based approach is used. You'll see that Alice and Bob establish an EPR pair with each other, using the quantum link (or links) between them.

When they successfully created this pair, both Alice and Bob do a measurement on a basis that they choose randomly, and independently from each other. They choose between the X- and Z- basis. If Alice or Bob want to measure in the Z-basis, they can immediately apply a measurement operation on their local qubit. The measurement will destroy this qubit but yield a classical bit as an outcome. If they want to measure in the X-basis, they first have to do a local transformation on their qubit. This is done by Hadamard gate. The subsequent measurement operation is then effectively a measurement in the X-basis.

Alice and Bob repeat this process (of creating an entangled pair, and locally measuring their qubits to obtain a classical bit) n times. In the Editor, you can choose the value of n.

When they are finished with all n iterations, Alice and Bob first throw away the measurement results of EPR pairs where they chose a different basis. To know which outcomes to throwing away, Alice and Bob send each other a list of bases that they measured their qubits in. In the Editor, you'll see this as a list of tuples (i, b) where i is the index of the qubit, and b is the basis they measured in (0 = Z, 1 = X).

At this point, Alice and Bob have a number of measurement outcomes left. In an ideal world, these outcomes are exactly the same between Alice and Bob, because of the nature of EPR pairs. In practice, however, there will be errors (differences) because of imperfect hardware, or potentially an eavesdropper. To estimate this Quantum Bit Error Rate (QBER), Alice and Bob will compare a subset of their measurement outcomes. For this, Alice sends a message with indices to Bob saying which outcomes to compare. They then send the measurement outcomes of these qubits to each other.

The measurement outcomes that they did not compare with each other, is their raw key. Note that Alice's raw key might not quite match Bob's raw key. Typically, at this point, Alice and Bob continue with more classical post-processing, including error correction and privacy amplification. The result of this post-processing is a secret key that is the same for Alice and Bob. The QBER gives an upper bound on the length of the secret key that can be extracted using post-processing.

In the Editor, you can choose the number of EPR pairs Alice and Bob will generate. The more EPR pairs they generate, the more classical bits they will obtain. This allows them to better estimate the error rate, and also extract a longer secret key. In a real setting, Alice and Bob would want to generate thousands of EPR pairs to get a useful key out of it.

The results screen displays various things, including the measurement bases Alice and Bob chose, their measurement outcomes, and whether they were compared with each other. The final results here are the raw key of Alice and Bob.

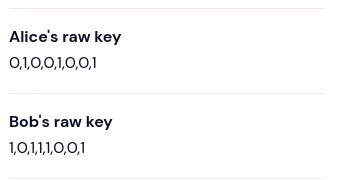
As mentioned above, in a real setting Alice and Bob would continue with post-processing this raw key until they have a shared, secret key. The QBER gives an indication of the length that the final secret key can have. In the results, this is shown as the key rate: the length of the final key divided by the length of the raw key.