State Teleportation

The purpose of quantum state teleportation is to send a quantum state from one location to another. Suppose that there is a person, Alice, who has a special quantum state, which she needs to send to a second person, Bob. Quantum teleportation makes it possible for Alice to send Bob her exact state, even if the state is completely unknown to her. In the state teleportation application that can be run in the Editor, you will get to choose the quantum state that Alice needs to send.

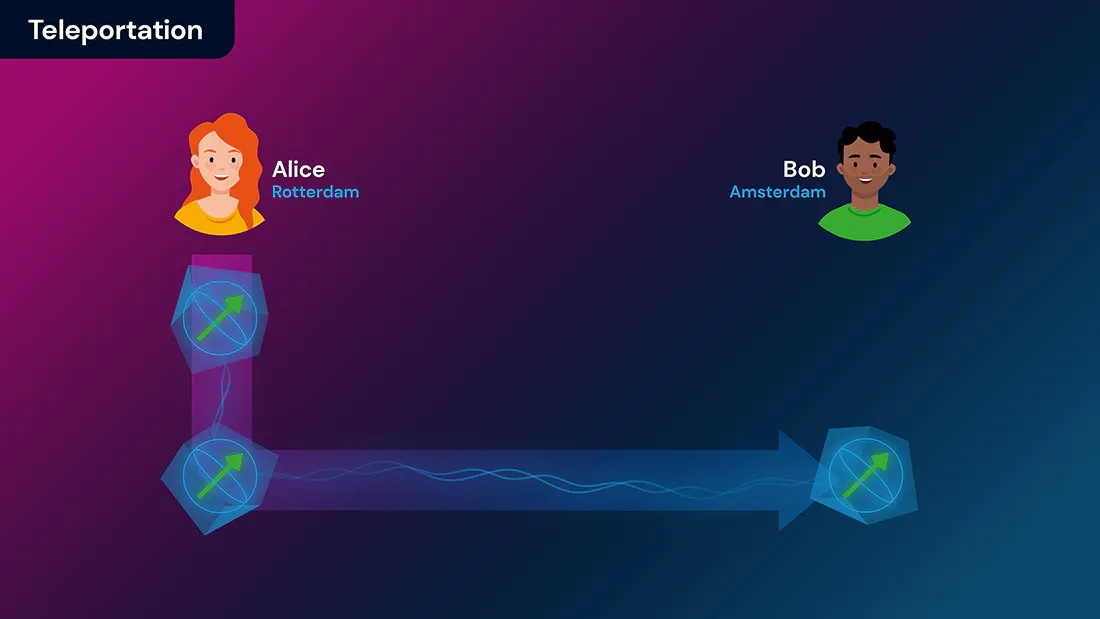
In order to perform this protocol, Alice must have two quantum systems, called qubits, and Bob must also have one. For Alice, the first of these systems is the secret state she wishes to send. Before beginning the protocol, Alice must collaborate with Bob over the quantum internet to create a shared entangled state, between her second qubit and his qubit. The shared state is called an EPR-pair and is consumed as a resource during the protocol.

In addition to consuming the resource state, this procedure costs Alice two uses of a classical communication channel, which she uses to send two classical bits of information to Bob. This means she communicates to him two numbers which can each be either zero or one.

In the state teleportation application that can be run in the Editor, the protocol begins by preparing the (user-defined!) quantum state to be sent to the receiver. To understand the preparation, it is helpful to think of the Bloch sphere. The state to be sent can be represented as a point on the Bloch sphere. On a sphere, one point can always be transformed into another by a series of rotations about two orthogonal axes, such as the Z and X axes. So to turn the initial quantum state into the state to be sent, you will see that rotations about two axes are performed.

Since the protocol requires that the sender and receiver use a shared entangled state as a resource, the next step of the protocol is to use the quantum network link (or links) to create an entangled pair between the sender and receiver.

Pro-tip: An encoding of a special quantum state is a different state from which, given additional information, it is possible to recover the special state. Recovering the special state from the encoding is called decoding. You can think of decoding as using the correct key to open a locked box.

Once an entangled pair has been created, it is time to start sending the quantum state you defined. Sending the state has four parts:

1. The sender does a CNOT gate between their two qubits. This operation alters their half of the entangled pair, conditioned on the value of the state to be sent. The point of this step is to ‘encode’ the state to be sent into their half of the entangled pair.

2. The sender does a Hadamard (abbreviation h) gate on the qubit that was originally to be sent. The point of this step is to move the encoding of the state to be sent from the sender's half of the entangled pair to the receiver's half.

3. The sender measures both of their qubits. The first reason for this step is that it leaves the receiver with an encoding of the state that they were supposed to receive, consuming the entanglement of the shared pair in the process. The second reason is that the measurement results tell the sender which quantum operations the receiver should do to correctly decode the quantum state that was sent to them.

4. Finally, the sender tells the receiver the measurement results, so that they will know which quantum operations they should do to decode the state they were sent.

Fun Fact: In general, if a quantum state is unknown and there are no extra copies of the state, then it is impossible to learn what the state is--to do so would require many copies, measured one after another. This means that if Alice has a single unknown state to send to Bob, the possibility of figuring out what it is and then telling him about it is completely ruled out. Instead, quantum teleportation allows Alice to send the state without even learning anything about it!

In the editor, you can choose the quantum state to be teleported, by specifying the angles that describe it in the Bloch sphere picture.

In real life, quantum teleportation is often used when the sender does not know the Bloch sphere description of the state they are sending.

In the results page of the editor, you will see a Bloch sphere representation of the quantum state that you chose to teleport as well as a second Bloch sphere indicating the quantum state recovered by the receiver at the end of the protocol. How well these two states match up is quantified by the fidelity, which is also shown here. If the fidelity is less than 1, then the two states do not match perfectly and one or more errors occurred during the protocol.

The measurement results sent to the receiver and the corresponding corrections made by the receiver are displayed as well.